Every Math DLL (MLL) must have at least the following entry point:
extern "C" MATHEXPORT void MATHCALL MathEntry( int iCommandCode, BOOL
bInit, MathEntryParam *pMathEntry )
Parameter Description:
| int iCommandCode | A command code that contains a value != 0, when a custom user menu is invoked; on normal invocation it contains 0 |
| BOOL bInit | A bool variable that contains true, when the MLL is invoked for the first time or "Restart" was called; false, when "Evaluate" was called or another operation triggered "Evaluate" |
| MathEntryParam *pMathEntry |
A pointer to the MathFrame entry interface; this interface allows to get the MathFrame environment by the following call:
This allows for binary backward compatibility of new MathFrame versions to old MLLs. |
The following header is needed:
#include <MathEnv.h>
MathFrame provides support for iostream style console output. For this to work, it is necessary to define MATH_IOSTREAM before the inclusion of MathEnv.h:
#define MATH_IOSTREAM
#include <MathEnv.h>
Furtheron it is necessary to connect the global wout object that will be automatically defined to the MathFrame environment by the following call:
wout.SetEnv( pEnv ) ;
In the following calls like the following are possible:
wout << "Hello world: " << 4711 << endl ;
The actual code will normally allocate resources, do some calculations, display the results of the calculations, cleanup the resources and then leave the MathEntry function. By the time the MathEntry function completes all the resources should be freed, since there need not be another invocation of MathEntry - this style of programming is quite similar to old fashioned C-style programs using a "main" entry function.
One of the main differences is the fact that an MLL is a DLL (dynamic link library), not an EXE (an executable program). Consult your compiler documentation on details how to create a DLL. For Visual C++, a batchfile that creates a DLL is provided in the "Template" directory. A typical compiler invocation might be:
cl -LD -GX -I..\include -FeTest.mll Test.cpp
Thats all there is to do - start MathFrame and load the newly created DLL.
This DLL is not yet very interesting - a next step might be to get some user specified parameters. This can be done by the following call:
MathParam *pParams = pEnv->GetParameters( bInit ) ;
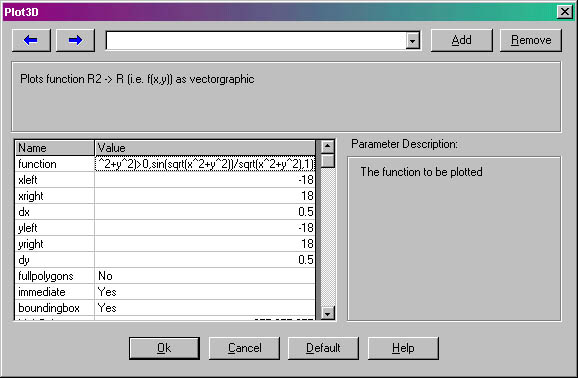
This creates an allocates a MathParam object; it displays a dialog that contains a table of named parameters as defined by a user provided XML description file. The use can then enter and edit the parameters; when done, the parameters can be retrieved by the program from the MathParam object. The dialog might look like:

If the bInit parameter is false, the dialog is not displayed; instead the MathParam object containing the unchanged parameters is returned. Typically the bInit parameter from the MathEntry routine will be passed here - this allows for not displaying the dialog, when Evaluate is called, which may be beneficial, especially when "Evaluate" is invoked automatically (e.g. by resizing a 2D Graphics window, while "AutoEvaluate" is set)
The XML description file normally has the extension ".DAT" and the same name as the MLL. E.g.: Test.MLL will call upon Test.DAT
This can however be overridden, especially if more than one such dialog with different parameter sets shall be displayed, like so:
MathParam *pParams = pEnv->GetParameters( bInit, "Alternate.DAT"
) ;
The XML file itself has a format like the following (this example produces the dialog as shown above):

See DAT File Reference on details.
To access the parameters in the MLL, use code like the following:
double xleft, xright, yleft, yright, dx, dy ;
MATHCOLOR highColor, lowColor ;
char achFunction[256] ;
xleft = pParams->GetValueDouble( "xleft" ) ;
xright = pParams->GetValueDouble( "xright" ) ;
yleft = pParams->GetValueDouble( "yleft" ) ;
yright = pParams->GetValueDouble( "yright" ) ;
dx = pParams->GetValueDouble( "dx" ) ;
dy = pParams->GetValueDouble( "dy" ) ;
highColor = pParams->GetValueColor( "highColor" ) ;
lowColor = pParams->GetValueColor( "lowColor" ) ;
bool bFull = pParams->GetValueBool( "fullpolygons" ) ;
bool bImmediate = pParams->GetValueBool( "immediate" ) ;
bool bBB = pParams->GetValueBool( "boundingbox" ) ;
pParams->GetValue( "function", achFunction, sizeof(achFunction)
) ;
As this example shows, the code knows, what parameter is of what type and calls the according functions with the names of the parameters.
This functioniality alone is already a good reason to use MathFrame for scientific code - it allows to quickly play with different values of parameters; since the parameter entry dialog also has a history feature that allows to identify and retrieve old parameter sets, it is very easy to compare the effects of different parameters.
For more difficult setups there is also a "file" parameter, that allows to browse for a filename, that identifies a file that can be opened and read by the MLL afterwards.
Finally, to make the MLL even more interesting, we do output some graphics; for the moment we will stick to a 3D poylgon graphics - bear in mind, that we could also make use of 2D pixel graphics and 2D vector graphics.
Every MLL can currently open one 2D graphics window and one 3D graphics window additionally to the console window (that is opened unconditionally). This could be done with code like the following:
pEnv->InitGraphics3D( MATHRGB(0,0,0), MATHRGB(0,255,0) ) ;
This opens the graphics window and initializes the default foreground and background color (black and green respectively).
To clear the screen from each and every data use:
pEnv->ClearScreen() ;
Now, if we want to draw a quad in 3-dimensional space, we could use something like:
pEnv->SetQuad3D( x, fval, y,
x+dx, f( x+dx, y ), y,
x+dx, f( x+dx, y+dy ), y+dy,
x, f( x, y+dy ), y+dy ) ;
Here f denotes a C-function that calculates a function, given an x and an y value.
To draw the outlines of such a polygon we could use:
pEnv->MoveTo3D( x, fval, y ) ;
pEnv->LineTo3D( x+dx, f( x+dx, y ), y ) ;
pEnv->LineTo3D( x+dx, f( x+dx, y+dy ), y+dy ) ;
pEnv->LineTo3D( x, f( x, y+dy ), y+dy ) ;
pEnv->LineTo3D( x, fval, y ) ;
The output of such a program might look similar to the following:

For a more detailed description of the API see: MathFrame API Reference
This ends our little introduction into the features of MathFrame.